Zuzanna K. Filutowska (Platyna) – Blog Osobisty

Ciąg Fibonacciego i złota proporcja w naturze

Dawno nie pisałam ale za to dzisiejszy wpis będzie długi i będzie nieco inny niż większośc wpisów na ten temat jakie udało mi się znaleźć w polskim internecie. Wpis ten jest komentarzem do filmiku zamieszczonego na Youtube przez Mirosława Zelenta:

Celem tego wpisu jest uświadomienie jak wiele pseudonauki i fałszywych informacji można zawrzeć w jednym filmiku na Youtube, które dla wielu osób stało się źródłem wiedzy o świecie.

Jeden z moich wykładowców – zoolog prof. Czesław Błaszak lubił powtarzać iż w naturze nie ma złotych reguł. Richard Feynman zaś twierdził, że przyroda jest absurdalna i że jest co całkowite zgodne z doświadczeniem, wyraził więc nadzieję iż ludzie zaakceptują naturą taką jaka jest – absurdalną.

Stad właśnie każdy szanujący się biolog, chemik czy fizyk będzie sceptycznie odnosił się do wszelkich “złotych reguł”. Od złotych reguł niedaleko jest od dogmatów. Przykładem w biologii molekularnej był tzw. centralny dogmat mówiący iż z DNA informacja płynie do RNA i dalej do białka. Odkrycie retrowirusów (w których informacja przepływa z RNA do DNA), prionów i mechanizmów epigenezy (gdzie nośnikiem informacji są białka – ale uwaga – jest to kwestia dyskusyjna) skłoniło naukowców do rewizji tego stwierdzenia.

Pan Mirosław Zelent pisze o sobie iż jest programistą i nauczycielem w szkole średniej. Powiem szczerze iż nieco mnie to przeraża, biorąc pod uwagę to co jest zawarte w tym filmiku. Maria Skłodowska-Curie pisała iż w nauce liczą się fakty a nie ludzie, tak więc zgodnie z tą maksymą skupię się na komentarzu do tego co p. Zelent powiedział i napisał (filmik ten składa się ze slajdów). Błędów merytorycznych w tym filmiku jest tak wiele iż naprawdę trudno będzie je wszystkie skomentować w jednym wpisie.

Przypomnijmy: ciąg Fibonaciego jest to ciąg liczb, z których każdy kolejny element ciągu jest sumą dwóch poprzednich: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

P. Zelent pisze iż liczba płatków kwiatów “w przytłaczającej większości jest liczbą Fibonacciego”. Prawda jest taka iż jest to bardzo “naciągane” stwierdzenie. Liczba płatków kwiatów często wynosi 0 2, 3, 4 lub 5. Mówi się iż u dwuliściennych jest to zwykle 5 u jednoliściennych 3 w okółku. Okółków może być więcej niż jeden – tak jest np. u jasnotowatych (Lamiaceae). Z tego co wiem z wykładów z botaniki systematycznej jest to dydaktyczne uproszczenie ponieważ całe rodziny roślin wyłamują się z tego schematu. Np. jaskrowate (Ranunculaceae) – zwykle mają 5 płatków ale duża część z nich ma 6, 7 i 8, inna duża rodzina – kapustowate (Brasicaceae) mają 4 (stąd ich dawna nazwa – krzyżowe), makowate (Papaveraceae) mają od 2 do 6 płatków itd. itd. Wiele roślin w ogóle nie ma płatków albo są one zrośnięte lub w inny sposób przekształcone. P. Zelent podał liczne przykłady, które mają ilustrować tę zależność więc do nich się odniosę.

• Kantedeskia (lilia Calla) – to co p. Zelent nazywa płatkiem jest tak naprawdę
  przekształconym liściem. Kwiaty roślin z rodziny obrazkowych (Araceae) mają najczęściej zredukowany okwiat (czyli 0 płatków), są bardzo małe i osadzone na kwiatostanie nazywanym kolbą (kwiatostan jest to wyspecjalizowana część pędu, na której osadzone są kwiaty). Ta kolba to właśnie ta żółta
  struktura, którą możemy zobaczyć na obrazku poniżej, otacza ją biały…no właśnie…nie jest to płatek lecz przekształcony liść podtrzymujący kwiatostan (taki liść nazywany jest w botanice podsadką).

  

• Wilczomlecz – dokładnie tak samo jak z Kantedeskią – z tym że kwiaty, tworzące tutaj inny rodzaj kwiatostanu nazywany wierzchotką, również ze zredukowanym okwiatem są otoczone podsadką złożoną z dwóch liści. Taki kwiat ma specjalną nazwę – cyjacjum.

  

  Co ciekawe, do tego samego rodzaju należy wilczomlecz nadobny nazywany poisencją lub gwiazdą betlejemską. Zapraszam Czytelników do policzenia czerwonych liści na poniższym obrazku…

  

• Trójlist – znów to co w filmie nazwane jest płatkami to podsadki – tym razem
  trzy. Poza tym do tej samej rodziny należą gatunki mające też 4 podsadki i nie są to żadne wyjątki. Na rysunku widzimy trójlist jajowaty.

  

  Liliowce mają najczęściej 6 płatków – dotyczy to całej podklasy (oczywiście są wyjątki gdyż przyroda rzadko stosuje się dokładnie do ludzkich reguł). Z kolei irysy (kosaćce) i lilie mają 3 płatki okwiatu w dwóch okółkach – czyli razem 6 płatków.

• Jaskier i ostróżka – jaskrowate (Ranunculaceae) mają zazwyczaj 5 płatków – ale generalnie mogą mieć od 0 do ponad dwudziestu. I to również nie są rzadkie przypadki. Co ciekawe – ostróżka została podana jako przykład na 5 i 8 płatków.
• Krwiowiec – należy do rodziny makowatych (Papaveraceae), która ma z reguły 4 płatki (2 w dwóch okółkach) ten gatunek ma od 6 do 12 płatków, co widać na zdjęciu poniżej.

  

• Rubekia, popielnik, krostawiec, nagietek, stokrotka, aster, złocieniec, i dalej słonecznik – są roślinami z rodziny astrowatych, które dawniej, nie bez powodu, nazywano złożonymi – to co w filmiku jest nazywane kwiatem – jest tak naprawdę kwiatostanem tzw. koszyczkiem, na którym są osadzone dwa rodzaje bardzo drobnych kwiatów (rurkowe i języczkowe). Z kolei to co jest nazywane płatkiem jest tak naprawdę kwiatem tzw. języczkowym. Kwiatów obu rodzajów może być praktycznie dowolna ilość (w przypadku kwiatów języczkowych może to być nawet 0 – jak np. u rumianka bezpromieniowego – na obrazku poniżej).

  

  Ta zmienność tyczy się nawet osobników tego samego gatunku. I nie mówimy tutaj o jakiejś niewielkiej grupce, tylko o rodzinie, która liczy prawie 30 tysięcy gatunków, co zwłaszcza w świecie roślin, jest liczbą bardzo dużą. Najłatwiej budowę takich kwiatów wyjaśnić na przykładzie słonecznika – jeśli wyrwiemy “płatek” z “kwiatu” słonecznika to tak naprawdę będziemy trzymać w ręku pojedynczy kwiat języczkowy. Z kolei każde nasiono (“pestka”) słonecznika powstaje z jednego kwiatu rurkowego. Licząc najpierw płatki a następnie nasiona można, w przybliżeniu, uzyskać liczbę kwiatów na kwiatostanie – jest to liczba raczej bardzo duża, może ona sięgać kilku tysięcy. Na obrazku poniżej znajduje się Bidens torta – roślina ta posiada jeden z najprostszych kwiatostanów wśród astrowatych, kwiatów języczkowych jest zazwyczaj 4, 5 lub 6.

  

Autor filmiku, na podstawie powyższych przykładów, autorytatywnie stwierdza

“Prawidłowo rozwinięty kwiat, bez mutacji, powinien mieć zawsze liczbę płatków równą liczbie Fibonacciego”.

Jak widać jest to oczywista nieprawda a wręcz kłamstwo.

Dalej z kwiatów natychmiast autor przechodzi do liści, na przykładzie koniczyny wyjaśnia jak ciężko znaleźć roślinę o liczbie liści innej niż liczba z ciągu Fibonacciego. Tak naprawdę chodzi tu o listki a nie liście. Liście wielu roślin składają się z kilku do kilkudziesięciu elementów nazywanych listkami. Koniczyna ma trzy listki, to prawda, jednakże zdecydowana większość roślin
nie ma liczby liści ani listków równej liczbom z ciągu Fibonacciego. Np. marsylia (na obrazku poniżej) ma 4, kasztanowce mogą mieć 6 i więcej, robinia może mieć kilkanaście itd. itd.

Podobnie jest z liczbą liści i gałęzi – pokazane są wyidealizowane schematy – które praktycznie poza podręcznikami nie istnieją, najlepiej po prostu iść na spacer albo pooglądać zdjęcia w Internecie, i policzyć odgałęzienia różnych drzew, krzewów, bylin aby się o tym przekonać.

Kolejny poważny błąd to stwierdzenie, że kwiaty potrzebują światła do fotosyntezy stąd konieczność stosowania złotej proporcji – otóż zdecydowana większość kwiatów fotosyntezy nie prowadzi (istnieją bardzo nieliczne wyjątki). Poza tym nie znalazłam w źródłach naukowych żadnego powiązania z ciągiem Fibonacciego i wydajnością fotosyntezy.

Dalej poruszony jest problem rozmieszczenia liści na łodygach. Jest tu jasna sugestia że umieszczanie jednego liścia nad drugim nie występuje. Natura jednak “wymyśliła” bardzo wiele sposobów ułożenia liści na łodygach, w tym jeden nad drugim (światło nie zawsze musi padać na roślinę z góry). Inny sposób ułożenia liści, przedstawiony jako niedobry to ułożenie jeden naprzeciwko drugiego (ułożenie naprzeciwległe), który również występuje u wielu roślin. Istnieje też
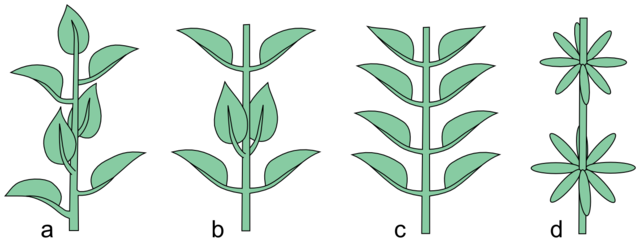
też ułożenia nakrzyżległe i okółkowe, które również nie spełniają zasad złotej proporcji i nie mają nic wspólnego z ciągiem Fibonaciego, złotymi kątami, spiralami itd. Ułożenie skrętoległe, które tak zachwala autor filmiku jest tylko jednym ze sposobów organizacji ulistnienia i nie zawsze (acz de facto zazwyczaj) spełnia omawiany ciąg. Wszystkie podane typy ulistnienia rozwijają się z merystemów. Samo istnienie i rozwój z merystemu nie jest tu żadnym dowodem. Poniższy rysunek przedstawia ulistnienie, odpowiednio skrętoległe, nakrzyżległe, naprzeciwległe i okółkowe.

Co do huraganów i galaktyk – nie jestem ekspertem więc nie mogę się na ten temat autorytatywnie wypowiadać. Obszary zakreślone “złota spiralą” wydają się jednak nie obejmować całości fenomenu – w ten sposób mogłabym nawet wpisać sobie w galaktyki czy huragany dowolną spiralę. Można powiedzieć iż przypominają one “złotą” spiralę…ale ma to takie same znaczenie dla nauki jak sławna twarz na Marsie.

Podobnie położenie Księżyca na Ziemi i mierzenie odległości między ich środkami wydaje mi się czystą numerologią. Przecież w naturze Księżyc nie spoczywa na Ziemi. Biorąc pod uwagę iż przypuszcza się że księżyc powstał z dysku akrecyjnego – tak jak Ziemia – zależność ta wydaje się kompletnie losowa.

Podobnie jest z naszym układem planetarnym – autor wziął pod uwagę planetę karłowatą Ceres (nie Seres) – zapewne aby potwierdzić swoją hipotezę. Dlaczego więc nie wziął Pan Plutona, Haumei, Makemake czy Eris? Zapewne dlatego iż wtedy odległość pomiędzy ich orbitami by nie spełniała złotej
proporcji. To już zakrawa na manipulację danymi – a to niezbyt ładne postępowanie.

Dalej ukazany jest krocionów – nie wiem czy autor zdaje sobie sprawę iż nie zawsze się zwija w taki sposób jak na zdjęciu – i normalnie porusza się, tak jak na zdjęciu poniżej, nie będąc zwiniętym w spiralę?

Podobnie ze ślimakami – ich muszla raczej nie przypomina spirali Fibonacciego…

Ten cały blok tekstu to komentarz jedynie do pierwszego rozdziału tego filmiku czyli około 7 minut. Błędne założenia, niepotwierdzone dane i występują praktycznie co kilka sekund.

Trudno nie wspomnieć o braku źródeł lub źródłach cokolwiek nieprzystających do etosu ani nauczyciela ani miłośnika nauki. Np. w rozdziale drugim autor filmiku stosuje jako (jedyne) źródło stronę niejakiego Haruna Yahya aka Adnana Oktara, który uważa iz holokaust jest syjonistycznym kłamstwem, jest on również propagatorem islamskiego kreacjonizmu i stosuje wywody na temat złotej proporcji jako dowody na to że świat jest dziełem inteligentnego projektu Allaha. Prowadzi też stronę pt. ewolucyjne oszustwo (evolutiondeceit.com) gdzie udowadnia iż ewolucja jest bezpośrednim powodem materializmu, komunizmu, nazizmu. Twierdzi również iż jeśli wszyscy bedą muzułmanami to nie będzie powodu do aktów terroru (szkoda tylko, że poszczególne odłamy islamu o tym nie wiedzą i nadal walczą ze sobą). Już nie wspominając o tym, że pomiary ciała są wykonywane źle np. ramiona są mierzone zwykłą linijką, ok. 5 cm nad łokciem na człowieku ubranym w luźny ubiór. Pomiary, które sprawdziłam na sobie np. palców znacznie odbiegają od złotej proporcji np. stosunek długości mojego środkowego i małego palca wynosi 1,45 a nic mi nie wiadomo o tym abym była zdeformowana.

Dalej autor mówi o DNA, ta część również opiera się na stronie Oktara i zawiera liczne błędy np. pada stwierdzenie “spirala DNA”. Otóż spirala ma się do helisy tak jak koło do kuli. Spirala jest strukturą dwuwymiarową a helisa zaś trójwymiarową. Dalej możemy się dowiedzieć iż “spirala” DNA ma długość 34 angstremy. Otóż podana długość dotyczy 10 par zasad (“szczebelków”) dna umieszczonych jeden nad drugim – w przybliżeniu jest to długość jednego skrętu helisy. Istnieją jednak, w organizmam żywych, formy DNA, gdzie jeden skręt helisy zawiera mniej lub więcej par zasad. Helisa w najszerszym miejscu ma 21 angstremów…owszem 21 i 34 to liczby Fibonacciego ale helisa DNA w najwęższym ma 12 angstremów…co więc z tym naszym 12, które liczbą Fibonaciego nie jest? Tego nam niestety autor nie mówi.

W końcu pojawia sie obrazek pochodzący z publikacji The hallmarks of cancer, przedstawiający artystyczną kompozycję zdjęć jednej komórki przechodzącej podział komórkowy. Tak się składa iż jest ona ułożona w spiralę, ale równie dobrze osoba wykonująca kompozycję mogł ułożyć te zdjęcia w okręg lub serduszko. Niestety poza przeczytanym opisem obrazka niczego się tu nie dowiemy…

Rozdział o muzyce zostawię bez komentarze, bo jak można skomentować występ komika jako dowód na boskość złotej proporcji?

W rozdziale nt. architektury, inżynierii itd. mamy przedstawione takie “dowody” jak na obrazku poniżej. Dlaczego ten a nie inny stopień schodów Partenonu został wzięty pod uwagę? Odpowiedź jest zapewne dla Czytelnika banalna – aby zgadzała się proporcja.

Oczywiście nie zabrakło też piramid, Mony Lisy i wielu, wielu innych rzeczy w tym logo Pepsi i Apple’a…

Rozdział nt. mistycyzmu również pominę gdyż, w mojej opinii, jest to czysta numerologia. Warto jednak zauważyć, że wśród tych sinusów i ułamków – tak naciągniętych by wynik wynosił Φ, mamy manipulację dotyczącą liczby 144000 w Apokalipsie wg Jana. Jako że liczba 144 jest liczbą Fibonacciego a 144000 już nie…trzy zera zostają po prostu obcięte aby zgadzało się to z wywodem.

Co do rozdziału nt. matematyki – nie jestem matematykiem – więc jedynie pobieżnie pozwolę sobie wypunktować swoje wątpliwości np. jeśli Φ wynos 1,618 a φ wynosi 0,618 to nijak nie kalkuluje mi się iż Φ + φ = 5.

Reasumując, autorytatywne, błędne i nieuźródłowione stwierdzenia powodują iż cała wypowiedź staje się praktycznie numerologią a nie nauką. Takie podejście było wielokrotnie krytykowane przez naukowców, w tym matematyków np.:
https://web.archive.org/web/20130501232006/http://www.maa.org/devlin/devlin_05_07.html
http://nautil.us/issue/0/the-story-of-nautilus/math-as-myth
http://wordplay.blogs.nytimes.com/2011/09/12/numberplay-phi-the-magic-and-the-myth/?_r=0

Oczywiście nie zaprzeczam iż złota proporcja i ciąg Fibonacciego występuje w naturze, ale na pewno nie jest on “tajemniczą regułą”. Przypuszcza się iż jest to zjawisko wynikające z prostego faktu że
akurat taki a nie inny układ dostarczał najlepszego dostosowania w danym przypadku. Jednakże w żadnym przypadku nie jest to reguła ani warunek sine qua non istnienia roślin – a tak usiłuje to p. Zelent przedstawić. Mało tego – można by napisać obszerną dysertację jeśli nie książkę, w której na przykładach można by udowadniać jak to natura ma szczególne “upodobanie” do ciągu liczb 1, 2, 3, 4, 5, 6, 7, 8, 9 i 10 (vide część na temat kwiatów i liści).

Układy biologiczne różnią się od układów znajdujących się w centrum zainteresowań czystej fizyki czy chemii tym, że wykazują cechy tzw. emergentne czyli takie, które wykazuje układ jako całość i które trudno prawidłowo opisywać za pomocą redukcjonistycznego podejścia (czyli prostych reguł czy zależności). Nie rozumiemy jeszcze tego jak te właściwości opisywać i uczy to nas pokory – zwłaszcza biologów molekularnych, biostatystyków i innych osób zajmujących się dziedzinami, których metodologia polega na podejściu redukcjonistycznym.

Na tym zapewne mógłby się mój wywód zakończyć…gdyby nie “epilog” zajmujący około 4 z 25 minut filmiku. Poza szczególnym użyciem słowa reminiscencja dowiadujemy się iż dowodu istnienia boga powinniśmy szukać w DNA, w którym jest zapisany “blueprint” złotej proporcji oraz że DNA samo się naprawia. Oprócz tego możemy się dowiedzieć iż autor, przypominam – nauczyciel w szkole średniej, jest kreacjonistą:

“Natura nie ma zdolności spontanicznego kreowania informacji lecz to informacja definiuje powstawanie materii, musi zostać zapisana jako pierwsza, stanowi podstawowy budulec świata, trzeba tu zapoznać się ze współczesną fizyką kwantową, teorią pola kwantowego i teorią strun czyli na początku jest słowo można by rzec parafrazując Biblię. Dla mnie to jest, największy “dowód” na inteligentne pochodzenia świata a nie jego spontaniczną kreację.

Dalej autor informuje nas że szkoły polskie są niedobre bo nikt mu nie powiedział o ciągu Fibonacciego ani w szkole podstawowej ani w liceum ani na studiach inżynierskich, magisterskich oraz doktoranckich (sic!). Tak się składa że ja też chodziłam do ośmioklasowej podstawówki i czteroklasowego liceum i powiedziano mi tam cóż to jest ciąg Fibonacciego. Z tego co udało mi się wyszukać ciąg Fibonacciego znajduje się w programie szkół ponadgimnazjalnych o czym nauczyciel informatyki i pokrewnych przedmiotów zawodowych, zwłaszcza ze stopniem doktora, powinien wiedzieć.

Sugerowałabym autorowi filmiku aby pozostał przy kursach programowania w C++, nieco podleczył swój naukowy obiektywizm, podejście do przyrody (zwłaszcza ewolucji) oraz nauki a co najważniejsze aby nie wypowiadał się na tematy, o których nie ma pojęcia, zwłaszcza iż jako nauczyciel autor odpowiada za tych, których naucza.

Please follow and like us: